streamalism.org

1. סקירה כללית

במאמר זה, אנו הולכים לחקור TreeMap הטמעה של מַפָּה ממשק מ- Java Collections Framework (JCF).

TreeMap הוא יישום מפות השומר על ערכי הערכים שלו לפי הסדר הטבעי של המפתחות, או יותר טוב באמצעות השוואה אם ​​המשתמש מסופק בזמן הבנייה.

בעבר סיקרנו מפת גיבוב ו LinkedHashMap יישומים ונבין שיש לא מעט מידע על אופן הפעולה של הכיתות האלה שדומה.

מומלץ לקרוא את המאמרים שהוזכרו לפני שתמשיך עם מאמר זה.

2. מיון ברירת מחדל TreeMap

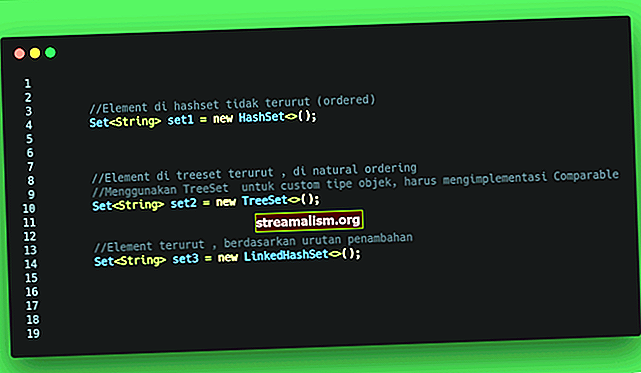
כברירת מחדל, TreeMap ממיין את כל הערכים שלו לפי הסדר הטבעי שלהם. עבור מספר שלם, פירוש הדבר יהיה סדר עולה ועל מיתרים, סדר אלפביתי.

בואו נראה את הסדר הטבעי במבחן:

@Test public void givenTreeMap_whenOrdersEntriesNaturally_thenCorrect () {TreeMap map = TreeMap new (); map.put (3, "val"); map.put (2, "val"); map.put (1, "val"); map.put (5, "val"); map.put (4, "val"); assertEquals ("[1, 2, 3, 4, 5]", map.keySet (). toString ()); }

שימו לב שהצבנו את מפתחות המספר השלם בצורה לא מסודרת אך עם אחזור מערך המפתחות, אנו מאשרים שהם אכן נשמרים בסדר עולה. זהו הסדר הטבעי של מספרים שלמים.

כמו כן, כאשר אנו משתמשים במחרוזות, הם ימוינו לפי הסדר הטבעי שלהם, כלומר אלפביתי:

@Test הציבורי בטל givenTreeMap_whenOrdersEntriesNaturally_thenCorrect2 () {מפת מפת Tree = מפת עץ חדשה (); map.put ("c", "val"); map.put ("b", "val"); map.put ("a", "val"); map.put ("e", "val"); map.put ("d", "val"); assertEquals ("[a, b, c, d, e]", map.keySet (). toString ()); }

TreeMapבניגוד למפת חשיש ומפת חשיש מקושרת, אינו משתמש בעקרון הגיבוב בשום מקום מכיוון שהוא אינו משתמש במערך לאחסון הערכים שלו.

3. מיון בהתאמה אישית TreeMap

אם איננו מרוצים מההזמנה הטבעית של TreeMap, אנו יכולים גם להגדיר כלל משלנו להזמנה באמצעות משווה במהלך בניית מפת עץ.

בדוגמה שלהלן, אנו רוצים שמספרי המפתחות השלמים יסודרו בסדר יורד:

@Test ציבורי בטל givenTreeMap_whenOrdersEntriesByComparator_thenCorrect () {מפת מפת Tree = TreeMap חדשה (Comparator.reverseOrder ()); map.put (3, "val"); map.put (2, "val"); map.put (1, "val"); map.put (5, "val"); map.put (4, "val"); assertEquals ("[5, 4, 3, 2, 1]", map.keySet (). toString ()); }

מפת hash אינה מתחייבת לסדר המפתחות המאוחסנים ובאופן ספציפי אינה מתחייבת כי הזמנה זו תישאר זהה לאורך זמן, אך מפת עץ מבטיחה כי המפתחות ימוינו תמיד לפי הסדר שצוין.

4. החשיבות של TreeMap מִיוּן

עכשיו אנחנו יודעים את זה TreeMap מאחסן את כל הערכים לפי סדר מיון. בגלל תכונה זו של מפות עצים, אנו יכולים לבצע שאילתות כמו; מצא "הגדול ביותר", מצא "הקטן ביותר", מצא את כל המקשים בערך מסוים פחות או יותר וכו '.

הקוד שלהלן מכסה רק אחוז קטן מהמקרים הבאים:

@Test הציבור בטל givenTreeMap_whenPerformsQueries_thenCorrect () {מפת מפת Tree = מפת TreeMap חדשה (); map.put (3, "val"); map.put (2, "val"); map.put (1, "val"); map.put (5, "val"); map.put (4, "val"); שלם הגבוה ביותר KeyKey = map.lastKey (); שלם הנמוך ביותר Key = map.firstKey (); הגדר keysLessThan3 = map.headMap (3) .keySet (); הגדר keysGreaterThanEqTo3 = map.tailMap (3) .keySet (); assertEquals (מספר שלם חדש (5), הגבוה ביותר); assertEquals (מספר שלם חדש (1), המפתח הנמוך ביותר); assertEquals ("[1, 2]", keysLessThan3.toString ()); assertEquals ("[3, 4, 5]", keysGreaterThanEqTo3.toString ()); }

5. יישום פנימי של TreeMap

TreeMap מכשירים NavigableMap ממשק ומבסס את עבודתו הפנימית על עקרונות העצים האדומים-שחורים:

בכיתה ציבורית TreeMap מרחיב את AbstractMap מיישמת NavigableMap, Cloneable, java.io.

העיקרון של עצים אדומים-שחורים הוא מעבר לתחום של מאמר זה, אולם יש לזכור דברים מרכזיים כדי להבין כיצד הם משתלבים TreeMap.

ראשית כל, עץ אדום-שחור הוא מבנה נתונים המורכב מצמתים; דמיין עץ מנגו הפוך עם שורשו בשמיים והענפים צומחים כלפי מטה. השורש יכיל את האלמנט הראשון שנוסף לעץ.

הכלל הוא כי החל מהשורש, כל אלמנט בענף השמאלי של כל צומת הוא תמיד פחות מהאלמנט בצומת עצמו. מימין תמיד גדולים יותר. מה שמגדיר יותר או פחות מנקבע על ידי הסדר הטבעי של האלמנטים או המשווה המוגדר בבנייה כפי שראינו קודם.

כלל זה מבטיח שהערכים של מפת עץ יהיו תמיד בסדר ממוין וצפוי.

שנית, עץ אדום-שחור הוא עץ חיפוש בינארי בעל איזון עצמי. מאפיין זה והאמור לעיל מבטיחים שפעולות בסיסיות כמו חיפוש, השגה, הצבה והסרה לוקחות זמן לוגריתמי O (יומן n).

להיות איזון עצמי זה המפתח כאן. ככל שאנו ממשיכים להכניס ולמחוק רשומות, דמיין את העץ הולך ומתארך בקצה אחד או קצר יותר בקצה השני.

פירוש הדבר שניתוח ייקח זמן קצר יותר על הענף הקצר יותר זמן על הענף שנמצא הכי רחוק מהשורש, דבר שלא היינו רוצים שיקרה.

לכן מקפידים על כך בעיצוב עצים אדומים-שחורים. לכל הכנסה ומחיקה, הגובה המרבי של העץ בכל קצה נשמר ב O (יומן n) כלומר העץ מאזן את עצמו ברציפות.

ממש כמו מפת חשיש ומפת חשיש מקושרת, מפת עץ אינה מסונכרנת ולכן הכללים לשימוש בה בסביבה מרובת-הברגה דומים לאלה שבשתי היישומים האחרים של המפה.

6. בחירת המפה הנכונה

לאחר שהסתכלתי מפת גיבוב ו LinkedHashMap יישומים בעבר ועכשיו TreeMap, חשוב לערוך השוואה קצרה בין השלושה כדי להנחות אותנו באיזה מהם מתאים לאן.

מפת חשיש טוב כמימוש מפות כללי המספק פעולות אחסון ושליפה מהירות. עם זאת, הוא נופל בגלל סידור הכניסות הכאוטי והבלתי מסודר שלו.

זה גורם לו לבצע ביצועים גרועים בתרחישים שבהם יש הרבה איטרציה שכן כל היכולת של המערך הבסיסי משפיעה על מעבר חוץ ממספר הערכים בלבד.

מפת חשיש מקושרת בעל התכונות הטובות של מפות חשיש ומוסיף סדר לערכים. זה מתפקד טוב יותר כאשר יש איטרציה רבה מכיוון שרק מספר הכניסות נלקח בחשבון ללא קשר ליכולת.

מפת עץ לוקח הזמנה לשלב הבא על ידי מתן שליטה מלאה על אופן מיון המפתחות. מהצד השני, הוא מציע ביצועים כלליים גרועים יותר משתי החלופות האחרות.

יכולנו לומר א מפת חשיש מקושרת מפחיתה את הכאוס בהזמנת מפת חשיש מבלי לספוג עונש ביצועים של מפת עץ.

7. מסקנה

במאמר זה חקרנו את ג'אווה TreeMap הכיתה והיישום הפנימי שלה. מכיוון שזה האחרון בסדרה של יישומי ממשק מפות נפוצים, המשכנו לדון בקצרה היכן הוא הכי מתאים ביחס לשניים האחרים.

קוד המקור המלא לכל הדוגמאות המשמשות במאמר זה ניתן למצוא בפרויקט GitHub.